In this notebook I decided to get more familiar with Julia basic functions, arrays, and operations by giving myself a small computational photography challenge! And on a suggestion, I played with the Interact.jl package too.

I’ve included the notebook I used for my image tiling manipulation, ending with playing with the Interact.jl library.

My notebook

In this notebook I want to take an image, break it into regions, and tile it with the maximum color from that region. It is an experiment in computational photography!

In [1]:
using Colors, Images, TestImages;

The one thing I find hard to get used to with Julia is that I don't need to explicitly call functions on module names, like in Python. Just a small detail, but I'll get used to it.

In [2]:
img = testimage("lighthouse");

Here's some documentation about Arrays, which are what images are represented as: http://docs.julialang.org/en/stable/manual/arrays/

In [3]:
# find the size of the image
println(size(img))
Out[3]:
(512,768)
In [4]:
summary(img)
Out[4]:
"512×768 Array{RGB{N0f8},2}"
In [5]:
# create a random dense array the same size as the image
# it gets initialized with random numbers, which makes a really cool pattern!
tiled_img = Array{RGB{N0f8}, 2}(size(img))
Out[5]:

Another way you can initialize an array like another:

In [6]:
tiled_img = similar(img);

Like in IPython, you can add a "?" at the end of a function. In Julia, you put the question mark at the start of a function.

In [7]:
?linspace
Out[7]:
search:

Iterating and Generating

There are many ways of generating a range of integers (that I will use to index into the image)

In [8]:
linspace(1, size(img, 1), 8)
Out[8]:
8-element LinSpace{Float64}:
 1.0,74.0,147.0,220.0,293.0,366.0,439.0,512.0
In [9]:
Int16.(linspace(1, size(img, 1), 8))
Out[9]:
8-element Array{Int16,1}:
   1
  74
 147
 220
 293
 366
 439
 512
In [10]:
Int16[i for i in linspace(1, size(img, 1), 8)]
Out[10]:
8-element Array{Int16,1}:
   1
  74
 147
 220
 293
 366
 439
 512

You can generate x, y tile indices with an interator-like thing or a generator-like thing.

In [11]:
# or to directly generate ints
1:8:size(img, 1)
Out[11]:
1:8:505
In [12]:
typeof(1:8:size(img, 1))
Out[12]:
StepRange{Int64,Int64}

And the visualizations for strips of images is awesome!

In [13]:
img[1:8:size(img, 1)]
Out[13]:

If you use these generators to index in both directions, what it basically does is tile the image and downsample.

In [14]:
stepsize = 16;
img[1:stepsize:size(img, 1), 1:stepsize:size(img, 2)]
Out[14]:
In [15]:
maximum(green.(img[1:10]))
Out[15]:
0.518N0f8
In [16]:
maximum(green.(img[1:16, 1:16]))
Out[16]:
0.533N0f8

And now let's put it all together to take the max R, G, and B values in a block.

In [17]:
for x in 1:stepsize:size(img, 1)
    for y in 1:stepsize:size(img, 2)
        x_end = min(x + stepsize, size(img, 1));
        y_end = min(y + stepsize, size(img, 2));
        # the @view takes a view into the image rather than making a copy
        imgv = @view img[x:x_end, y:y_end]
        tiled_img[x:x_end, y:y_end] = RGB{N0f8}(
            maximum(red.(imgv)), maximum(green.(imgv)), maximum(blue.(imgv)));
    end
end

And we can concatenate the images to put them size by side.

In [18]:
[img tiled_img]
Out[18]:

I can even put all this into a function to call separately. Small notes about functions:

  • Arguments can either be positional or keyword, but not both. The function below means I have to call stepsize= every time I want to pass stepsize.
  • The last statement is the object returned by the function.
In [19]:
function max_tiling(img; stepsize=16)
    tiled_img = similar(img);
    for x in 1:stepsize:size(img, 1)
        for y in 1:stepsize:size(img, 2)
            x_end = min(x + stepsize, size(img, 1));
            y_end = min(y + stepsize, size(img, 2));
            imgv = @view img[x:x_end, y:y_end];
            tiled_img[x:x_end, y:y_end] = RGB{N0f8}(
                maximum(red.(imgv)), maximum(green.(imgv)), maximum(blue.(imgv)));
        end
    end
    tiled_img
end
Out[19]:
max_tiling (generic function with 1 method)
In [20]:
[img max_tiling(img, stepsize=16)]
Out[20]:
In [21]:
[img max_tiling(img, stepsize=8)]
Out[21]:

I am told that the interact.jl package (https://github.com/JuliaGizmos/Interact.jl) can let me make a slider to change the stepsize!

In [22]:
for x in 1:stepsize:size(img, 1)
    for y in 1:stepsize:size(img, 2)
        x_end = min(x + stepsize, size(img, 1));
        y_end = min(y + stepsize, size(img, 2));
        imgv = @view img[x:x_end, y:y_end]
        tiled_img[x:x_end, y:y_end] = RGB{N0f8}(maximum(red.(imgv)), maximum(green.(imgv)), maximum(blue.(imgv)));
    end
end
In [23]:
# Pkg.add("Interact")
In [24]:
using Interact;
Out[24]:

The widget lets me manipulate the step size and re-generate images directly in the notebook! Highly recommend this package =)

In [25]:
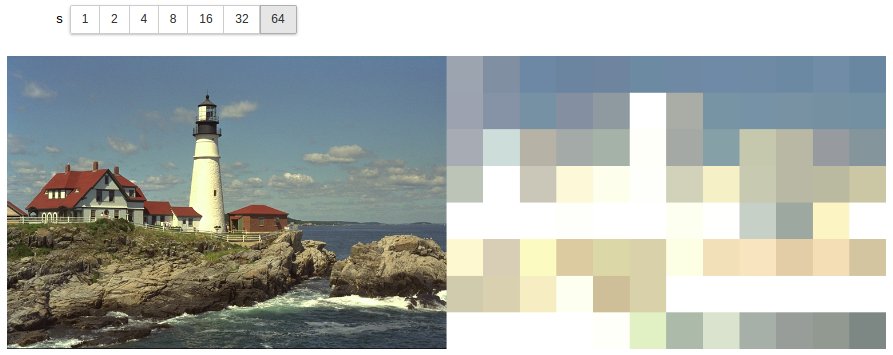
@manipulate for s=[2^x for x in 0:6]
    [img max_tiling(img, stepsize=s)]
end
Out[25]:

The widget in the last output of the notebook did not render properly, so I’m including a screenshot here:

Interact.jl widget

Random memory initialization

In line 4 (In[4]:), an uninitialized array takes random memory and random values. I don’t fully understand where this memory comes from, but I’m pretty sure it has to do with most-recently accessed memory. When I was running on my local machine, line 2 (In[2]:) loaded the original image of the lighthouse we saw in my first post. So when line 4 (creating a random uninitialized array) was executed, I got this pretty lighthouse artifact! You can see it is different image than came up in the second run of the notebook rendered above!

Random memory initialization

Jupyter notebook rendering aside

As another aside, in rendering the Jupyter notebook, the Interact library created widgets that generated custom Javascript during the nbconvert phase. I just removed that entire script section from the generated HTML, which is why I had to include a screenshot of the final widget at the end. I’m sorry for that ugliness - Jupyter and nbconvert are fantastic projects, they just can’t possibly cover all use cases!

Any comments for me?